图论(2)
最短路
最短路是非常常见的问题,有单源最短路和全源最短路,求解方法和各种应用也很多。来看一些常用、基本的最短路算法。
图的建立
- 用多个数组或一个结构体来直接存边。建图方便,操作效率低,在$Kruskal$算法中有应用。
- 邻接矩阵,$f[u][v]=w$表示$u$到$v$有一条权值为$w$的边。建图方便,遍历复杂度高,空间花费巨大,不适用于有重边的情况,一般用于稠密图,$Floyd$算法一般使用邻接矩阵。
- vector存边。建图方便,可对边排序,操作效率高。
- 链式前向星。类似邻接表,理解后背模板即可,操作效率高,后文代码均使用此方式建图。
单源最短路
单源最短路径指的是求从图上一个起点出发到其他所有点的最短路径。
以下默认一张图中$n$个点,$m$条边。
$Bellman-Ford$算法
Bellman-Ford算法最核心的操作是松弛操作,其思想为:用当前节点的最短路去更新其邻接点的最短路。
容易想到,一条最短路上最多只有$n$个点和$n-1$条边,因此我们只需要对每一条边尝试松弛$n-1$次,若存在最短路,则这些操作后一定找齐了所有的最短路,且所有边均不能再松弛操作;若仍能进行松弛操作,表示存在负环。
Bellman-Ford算法非常暴力,时间复杂度很高。显然,在对一条边进行松弛时,只有它的前驱节点已经进行过最短路的估计,即$dist[u]$不为$\infty$时,边$(u,v)$才能被松弛。在Bellman-Ford算法中,有大量的边在遍历时不需要被松弛。
我们可以利用队列进行优化得到$SPFA$算法。
$SPFA$算法
对于Bellman-Ford,将所有更新过的点加入队列,每次取出一个点进行松弛,直到队列为空,这就是$spfa$.
1 | void spfa(int s) |
但是即使使用队列优化过,$spfa$时间复杂度依然很高,最坏情况下达到$O(|V|\cdot |E|)$.很容易被卡掉。
负环判定
$spfa$的一个优点在于可以判别图中是否存在负环。判定方法是:记录每个点的入队次数,如果这个次数达到了总的节点数则说明图中存在负环。
注意是判入队次数而不是松弛次数,如果存在重边导致了多次松弛,会对松弛次数的判断产生影响,可能会被$hack$。
1 | if(dist[v]>dist[u]+w){ |
但是这种方法可能会爆$int$,原因在于要让入队次数达到$n$,则遍历的总个数最大可达$n^2$.
考虑换一种思路,如果不存在负环,那么从某点出发到每个点的最短路应当是不存在环的。因此我们可以判断最短路径的路径边数是否小于$n$(即经过点数小于等于n,没有任何一个点重复走过),来更高效地判断负环。
1 | if(dist[v]>dist[u]+w){ |
$Dijkstra$算法
$spfa$如此之慢,我们需要一种更快更稳定的最短路算法。
$dijkstra$算法的思想是贪心+$bfs$求最短路,它只适用于不含负边权的图。在稠密图中表现优秀。
我们将点分成两类,一类是已经确定最短路径的点,称为“白点”,另一类是未确定最短路径的点,称为“蓝点”。
$dijkstra$流程如下:
- 初始化$dist[s]==0$,其余节点的$dist$值为$\infty$.
- 找到一个$dist$最小的蓝点$u$,将节点$u$变成白点,即找到最短路。
- 遍历$u$的所有出边$(u,v,w)$,若$dist[v]>dist[u]+w$,则$dist[v]=dist[u]+w$.
- 重复$2,3$两步,直到所有点变成白点。
这样做的时间复杂度是$O(n^2)$。
图解
- 另初始节点$s$为1,把$dist[s]$初始化为0,其余点初始化为$\infty$.
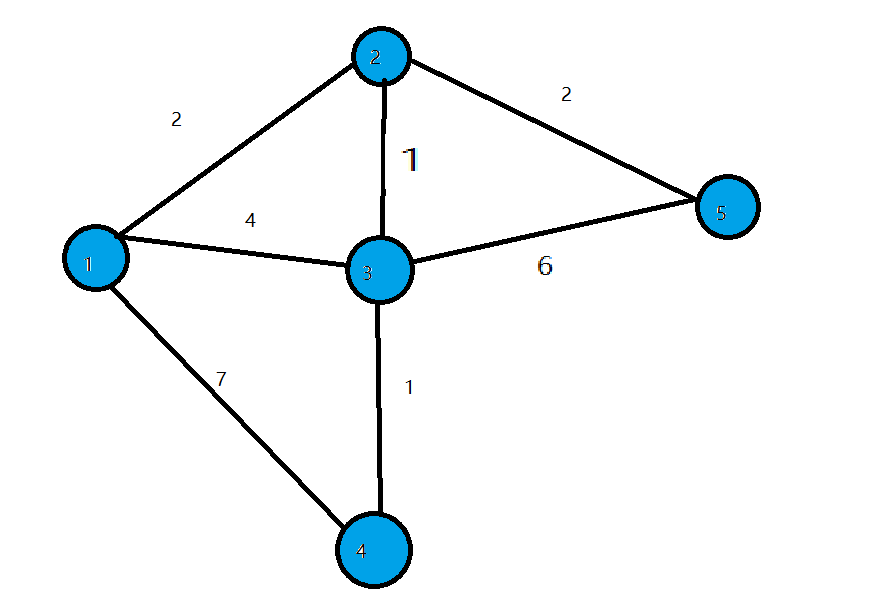
- 第一轮循环找到$dist$最小的点$1$,将$1$变成白点,对所有与$1$相连的蓝点的$dist$进行松弛,使$dist[2]=2,dist[3]=4,dist[4]=7$
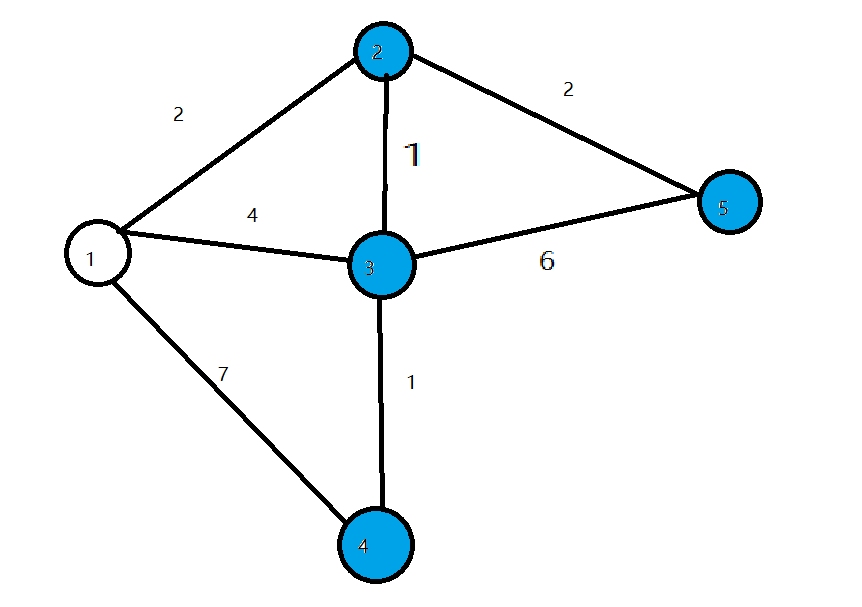
- 第二轮循环找到$dist$最小的点$2$,将$2$变成白点,对所有与2相连的蓝点的$dist$进行松弛,使$dist[3]=3,dist[5]=4$
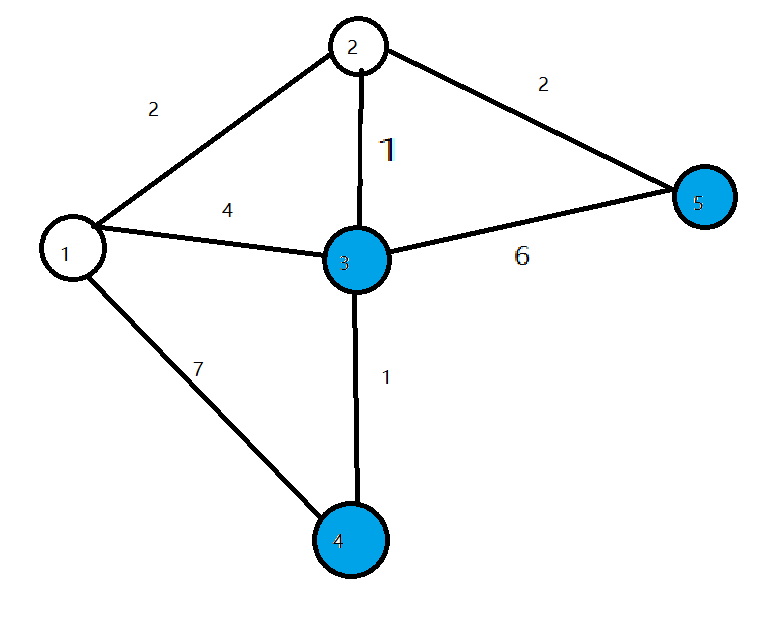
- 第三轮循环找到$dist$最小的点是$3$,将3变成白点,对所有与3相连的蓝点进行松弛,使$dist[4]=4$
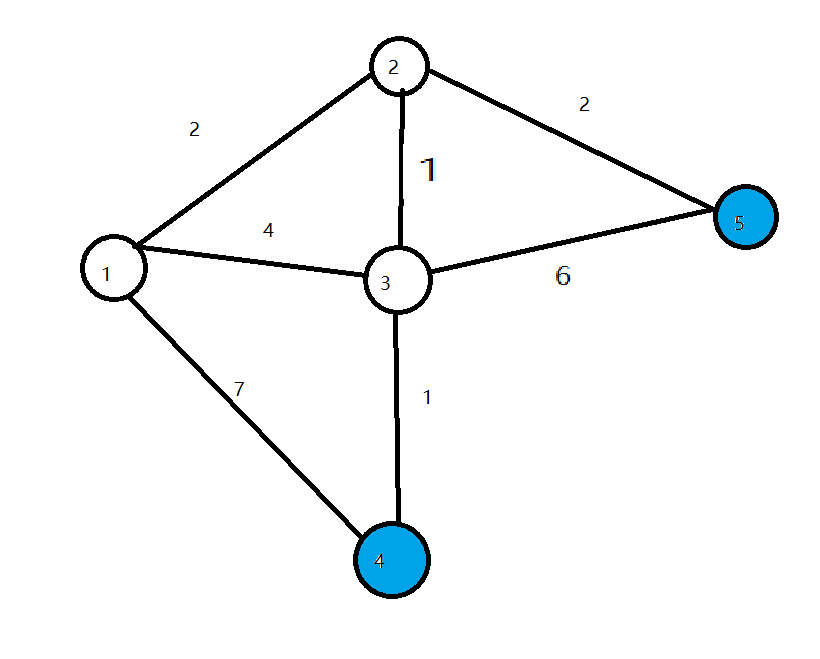
- 接下来两轮循环分别将4、5设置为白点,算法结束,所有点最短路径找到。
为什么$dijkstra$不能处理负边权图
- 我们来看下面这张图
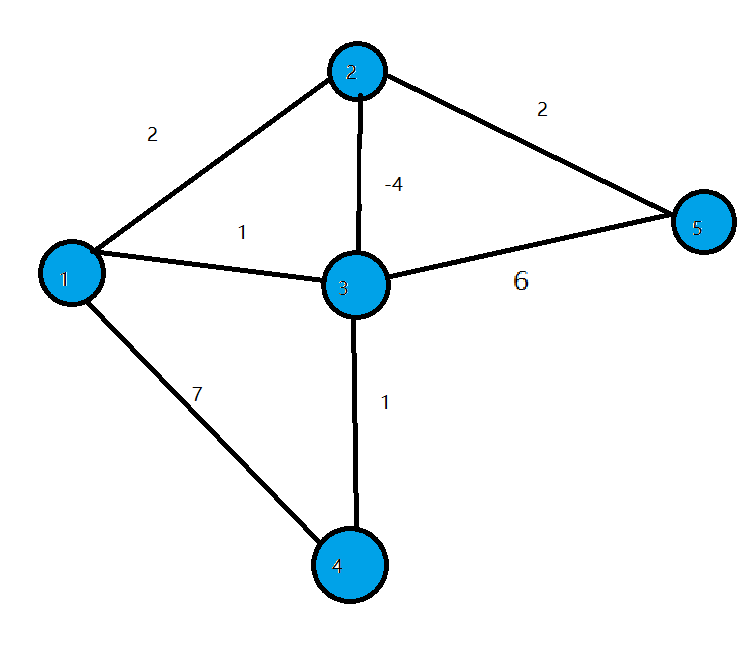
- 2到3的边权为-4,显然从1到3的最短路径为-2(1->2>3).但在循环开始时程序会找到当前$dist$最小的点3,并将其标记为白点。
- 这时$dist[3]=1$,然而1并不是起点到3的最短路径,且3已经被标记为白点,所以$dist[3]$不会再被修改。
- 我们在边权为负时得到了错误的答案。
$dijkstra$的堆优化
观察流程,发现步骤2可以优化。我们用小根堆对$dist$数组进行维护,在$O(\log n)$的时间取出堆顶元素并删除,用$O(\log n)$遍历每条边,总的时间复杂度为$O((n+m)\log n)$.
$dijkstra$的正确性
我们可以考虑反证法。假如点$u$在出队后优先队列中还有点$y$可以使$dist[u]$减小,那么$dist[y]$必然小于$dist[u]$.而根据优先队列的性质,$dist[u]$是堆中最小的元素,即$dist[u]\leq dist[y]$,产生矛盾。因此可以保证$u$出队后$dist[u]$是最小的。
1 | struct Node{ |
$DAG$图最短路
$DAG$图即有向无环图,可以直接对图进行拓扑排序,按照点的顺序一次进行松弛操作即可。
正确性
拓扑排序后松弛的顺序即是最终结果中最短路边的顺序,每次松弛前边的起点都已经找到最短路,满足最优子结构。
时间复杂度
线性
全源最短路
全源最短路径指求图上任意两点之间的最短路径。
常见算法包括$Floyd$算法、$Johnson$算法。
$Floyd$算法
$floyd$算法是一种动态规划求解最短路的方法,其基本思想是:对于每个起点和终点,枚举中间点,进行状态转移。
转移方程为$d_{x,y}=min(d_{x,k}+d_{k,y}|1\leq k \leq n)$
时间复杂度为$O(n^3)$
1 | for(int k=1;k<=n;k++) |
$floyd$算法还可以判断图中两个点是否连通,在数据范围较小时非常好用。
$Johnson$算法
$johnson$算法求任意两点间的最短路,是通过枚举起点,跑$n$次$dijkstra$算法解决,算法的时间复杂度为$O(nm\log m)$,在稀疏图上比$floyd$算法更加优秀。
但是$dijkstra$算法不能正确求解带负权边的最短路问题,因此我们需要在原图上做预处理,确保所有的边权非负。
一种任意想到的方法是给所有边的边权同时加上一个正数$x$,从而让所有的边权非负。如果新图上起点到终点的最短路经过了$k$条边,则将最短路减去$kx$得到实际最短路。
但这种方法是错误的。因为如果原图上最短路边数较多,再每条边加上正数$x$后,新图可能存在一条边数更少的最短路,这时已经不是原来的最短路了。
$johnson$算法通过另一种方法来给每条边重新标注边权。
我们建立一个超级源点(编号为$0$),从这个点向每一个点连一条权值为$0$的边。
首先可以用$spfa$求出源点到每个节点的最短路,记为$h_i$。
假设原图中存在一条从$u$到$v$,边权为$w$的边,我们将该边的边权重新设置为$w+h_u-h_v$。
接下来以每个点为起点,跑$n$轮$dijkstra$算法即可求出新图任意两点间的最短路。
以$u$为起点,$v$为终点的最短路结果求出为$dist[v]$,实际在原图上为$dist[v]+h_v-h_u$。
正确性证明
在重新标记的图上,从$s$点到$t$点的一条路径$s->p_1->p_2->\cdots ->p_k->t$的长度表达式为:
$(w(s,p_1)+h_s-h_{p_1})+(w(p_1,p_2)+h_{p_1}-h_{p_2})+\cdots +(w(p_k,t)+h_{p_k}-h_t)$
化简后得到:
$w(s,p_1)+w(p_1,p_2)+\cdots +w(p_k,t)+h_s-h_t$
无论我们走哪一条路径,$h_s-h_t$的值不变的。这类似于两点间势能差的概念,只与两点位置有关。
为了方便,下面我们就把$d_i$称为$i$点的势能。
新图中的$s->t$的最短路长度表达式有两部分组成,前面的边权和为$s$到$t$的最短路,后面为两点的势能差。因为两点间的势能差为定值,因此原图上$s->t$的最短路与新图上$s->t$的最短路相对应。
至此我们证明了重新标注后图上最短路径仍是原图上的最短路径,接下来需要证明标注后所有边权非负,因为在非负边权上,$dijkstra$才能保证得出正确的结果。
根据三角形不等式,新图上任意一边$(u,v)$满足:$h_v\leq h_u+w(u,v)$。这条边重新标注之后的边权为$w’(u,v)=w(u,v)+h_u-h_v\geq 0$。这样证明了标注后边权均非负。
至此我们证明了$johnson$算法的正确性。
上模板johnson全源最短路
1 |
|
差分约束系统
还不会
$K$短路
还不会
同余最短路
还不会