线段树与树状数组

线段树和树状数组是很常用的数据结构，用来处理区间问题，包括区间的修改和查询。

线段树

线段树，顾名思义，是将区间分成一段一段来进行区间操作。对于每个子节点，都表示整个序列的一段子区间；对于叶子节点而言，都表示序列中单个元素信息；子节点不断向自己的父亲节点传递信息，而父节点存储的信息是它每一个子节点信息的整合。

线段树可以维护支持结合律的数据，比如加和，乘法，最大/最小值。

如何进行分段？

考虑将区间$[l,r]$分成两半$[l,mid]、[mid+1,r]$​,相当于将区间对半分，对于每个区间都这样分段，最终段数为$O(n\log n)$.

当我们对区间$[l,r]$进行操作时，从最大的区间开始，从此去找对应操作的区间。

• $[l,r]$包含在当前节点的左区间内，接着往左区间走
• $[l,r]$​包含在当前节点的右区间内，接着往右区间走
• $[l,r]$​跨过当前节点区间的中点，左边操作$[l,mid]$​​,右边操作$[mid+1,r]$​

如此反复，直到找到的区间与操作区间一致，就进行操作。

线段树大致图像如下：

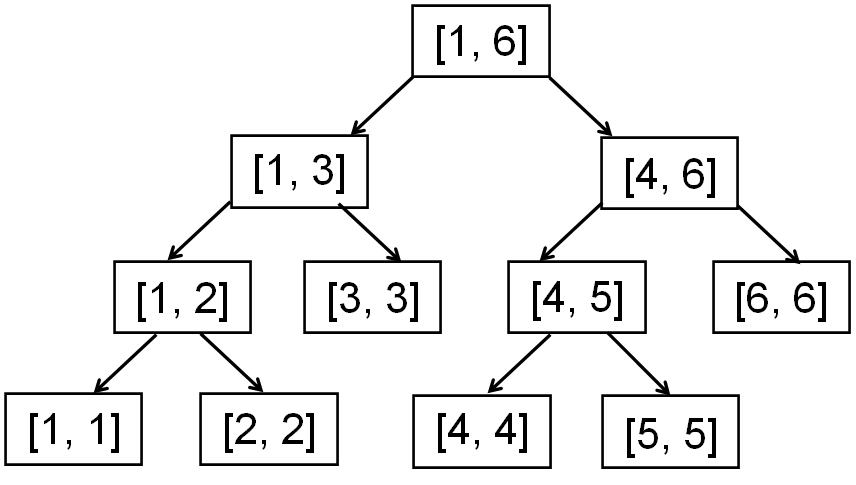
当涉及到区间的修改，如加减、乘除时，我们可以在找到的区间上打上懒标记($lazy tag$​),这样不用每次往下遍历整棵线段树。在进行修改和查询时要注意懒标记的下传，还要向上更新节点维护的值。

线段树1

懒标记的优先级

当区间的修改包括了加和乘时，需要设置两个标记，$add$加标记、$mul$乘标记。而这时候需要注意优先级问题。

先进行乘法后进行加法。

如果我维护的值是$a$，我的懒标记有$+b$​和$\times c$，可以发现$(a+b)\times c \neq a\times c+b$.

而在记录懒标记时，加法和乘法两种标记放到一起，需要确定一个优先级。

我们分析一下两种顺序：

• 先加后乘：$(a+b)\times c = a\times c+b\times c$
• 先乘后加：$a\times c+b$

上面先加后乘的式子相当于下面的式子，在加法上面多乘了一个$c$

所以，只要是先加后乘的式子，只要在$b$上$\times c$就可以转化为先乘后加的式子

具体操作是在添加乘法标记的时候，先将加法标记$\times c$即可

懒标记下传推导

在传递懒标记$pushdown$时

假设当前节点是$o$,$add[o]$是当前节点的加法标记，$mul[o]$是当前节点的乘法标记，$sum[o]$是当前节点维护的和，$ls$是左儿子的编号，$rs$是右儿子的编号。这里当前节点的值已经维护好，儿子还没维护好。

以左儿子为例，根据先乘后加的顺序，给左儿子乘上自己的乘法标记，再加上自己的加法标记。

$$sum[ls] = sum[ls]\times mul[o]+add[o]\times (r-l+1)$$

这样，左儿子的$sum$值就维护好了。那么如果儿子有懒标记呢？

如果儿子有懒标记，它的懒标记要维护一个值$s$，它维护后的值$s’$应该是

$$s’ = s\times mul[ls]+add[ls]$$

现在又要给它加上父节点$o$的懒标记，那么维护后的值应该是
$$
\begin{equation}\begin{split}
s’’&=s’\times mul[o] + add[o] \
&=(s\times mul[ls]+add[ls])\times mul[o]+add[o] \
&=s\times mul[ls]\times mul[o]+add[ls]\times mul[o]+add[o]
\end{split}\end{equation}
$$
如果$mul[ls]’,add[ls]’$是维护后的懒标记，我们就知道了懒标记应该怎么维护

$$mul[ls]’ = mul[ls]\times mul[o]$$

$$add[ls]’=add[ls]\times mul[o]+add[o]$$

在维护懒标记时，乘法标记乘以父节点的乘标记，加法标记先乘以父节点的乘标记，再加上父节点的加标记即可。

线段树2

模板

展开查看代码 >folded

#include <iostream>
#include <cstring>
#include <cmath>
#include <algorithm>
#include <queue>
#include <stack>
#include <vector>

#define INF 0x3f3f3f3f
using namespace std;
typedef long long ll;
const int maxn = 1e5 + 10;

inline ll read()
{
    ll x = 0, f = 1;
    char ch = getchar();
    while (ch < '0' || ch > '9')
    {
        if (ch == '-')
            f = -1;
        ch = getchar();
    }
    while (ch >= '0' && ch <= '9')
    {
        x = (x << 3) + (x << 1) + (ch ^ 48);
        ch = getchar();
    }
    return x * f;
}
struct node
{
    int l, r;
    ll sum, add, mul = 1; //该点维护的和，加标记，乘标记初始为1
} tree[maxn << 2];

ll a[maxn];
ll n, m, p;

inline int ls(int pos) { return pos << 1; }
inline int rs(int pos) { return pos << 1 | 1; }

//向上更新节点维护的和
void pushup(int pos)
{
    tree[pos].sum = (tree[ls(pos)].sum + tree[rs(pos)].sum) % p;
}

void build(int pos, int l, int r) //当前节点，操作区间
{
    tree[pos].l = l, tree[pos].r = r;
    if (l == r)
    {
        tree[pos].sum = a[l] % p;
        return;
    }
    int mid = l + r >> 1;
    build(ls(pos), l, mid);
    build(rs(pos), mid + 1, r);
    pushup(pos);
}
//向下传递懒标记
void pushdown(int pos)
{
    if (tree[pos].mul != 1)
    {
        //更新两个标记与节点维护的和,直接乘
        (tree[ls(pos)].mul *= tree[pos].mul) %= p;
        (tree[rs(pos)].mul *= tree[pos].mul) %= p;
        (tree[ls(pos)].add *= tree[pos].mul) %= p;
        (tree[rs(pos)].add *= tree[pos].mul) %= p;
        (tree[ls(pos)].sum *= tree[pos].mul) %= p;
        (tree[rs(pos)].sum *= tree[pos].mul) %= p;
        //已经传递，修改为1
        tree[pos].mul = 1;
    }
    if (tree[pos].add)
    {
        (tree[ls(pos)].add += tree[pos].add) % p;
        (tree[rs(pos)].add += tree[pos].add) % p;
        //左子树的sum值加上 节点数*懒标记
        (tree[ls(pos)].sum += (tree[ls(pos)].r - tree[ls(pos)].l + 1) * tree[pos].add % p) %= p;
        //右子树的sum值加上 节点数*懒标记
        (tree[rs(pos)].sum += (tree[rs(pos)].r - tree[rs(pos)].l + 1) * tree[pos].add % p) %= p;
        //已经传递，修改为0
        tree[pos].add = 0;
    }
}

//加法更新
void updateAdd(int pos,int l,int r,int k)
{
    if(tree[pos].l==l&&tree[pos].r==r){
        //更新该节点维护的和
        (tree[pos].sum += (r-l+1) * k % p) %= p;
        //更新该节点懒标记
        (tree[pos].add += k) %= p;
        return;
    }
    //注意要先pushdown!!!
    pushdown(pos);
    int mid = tree[pos].l+tree[pos].r>>1;
    //只在左儿子节点更新
    if(r<=mid) updateAdd(ls(pos),l,r,k);
    //只在右儿子节点更新
    else if(l>mid) updateAdd(rs(pos),l,r,k);
    //在左右儿子节点更新
    else updateAdd(ls(pos),l,mid,k),updateAdd(rs(pos),mid+1,r,k);
    //最后pushup!!!
    pushup(pos);
}

//乘法更新
void updateMul(int pos,int l,int r,int k)
{
    if(tree[pos].l==l&&tree[pos].r==r){
        //更新该节点维护的和
        (tree[pos].sum *= k) %= p;
        //更新该节点懒标记
        (tree[pos].add *= k) %= p;
        (tree[pos].mul *= k) %= p;
        return;
    }
    //注意要先pushdown!!!
    pushdown(pos);
    int mid = tree[pos].l+tree[pos].r>>1;
    //只在左儿子节点更新
    if(r<=mid) updateMul(ls(pos),l,r,k);
    //只在右儿子节点更新
    else if(l>mid) updateMul(rs(pos),l,r,k);
    //在左右儿子节点更新
    else updateMul(ls(pos),l,mid,k),updateMul(rs(pos),mid+1,r,k);
    //最后pushup!!!
    pushup(pos);
}

ll query(int pos,int l,int r)
{
    if(tree[pos].l==l&&tree[pos].r==r){
        return tree[pos].sum;
    }
    //注意先pushdown!!!
    pushdown(pos);
    int mid = tree[pos].l+tree[pos].r>>1;
    //只在左儿子节点查询
    if(r<=mid) return query(ls(pos),l,r);
    //只在右儿子节点查询
    else if(l>mid) return query(rs(pos),l,r);
    //在左右儿子节点查询
    else return (query(ls(pos),l,mid)+query(rs(pos),mid+1,r))%p;
}

int main()
{
    cin>>n>>m>>p;
    for(int i=1;i<=n;i++)
        a[i] = read();
    build(1,1,n);
    while(m--)
    {
        int opt;
        ll x,y,k;
        opt = read(),x = read(),y = read();
        if(opt==1){
            k = read();
            updateMul(1,x,y,k);
        }
        else if(opt==2){
            k = read();
            updateAdd(1,x,y,k);
        }
        else if(opt==3){
            printf("%lld\n",query(1,x,y));
        }
    }
    return 0;
}

树状数组

单点修改，区间查询

树状数组用于维护前缀和，可以单点修改。

大致图像如下

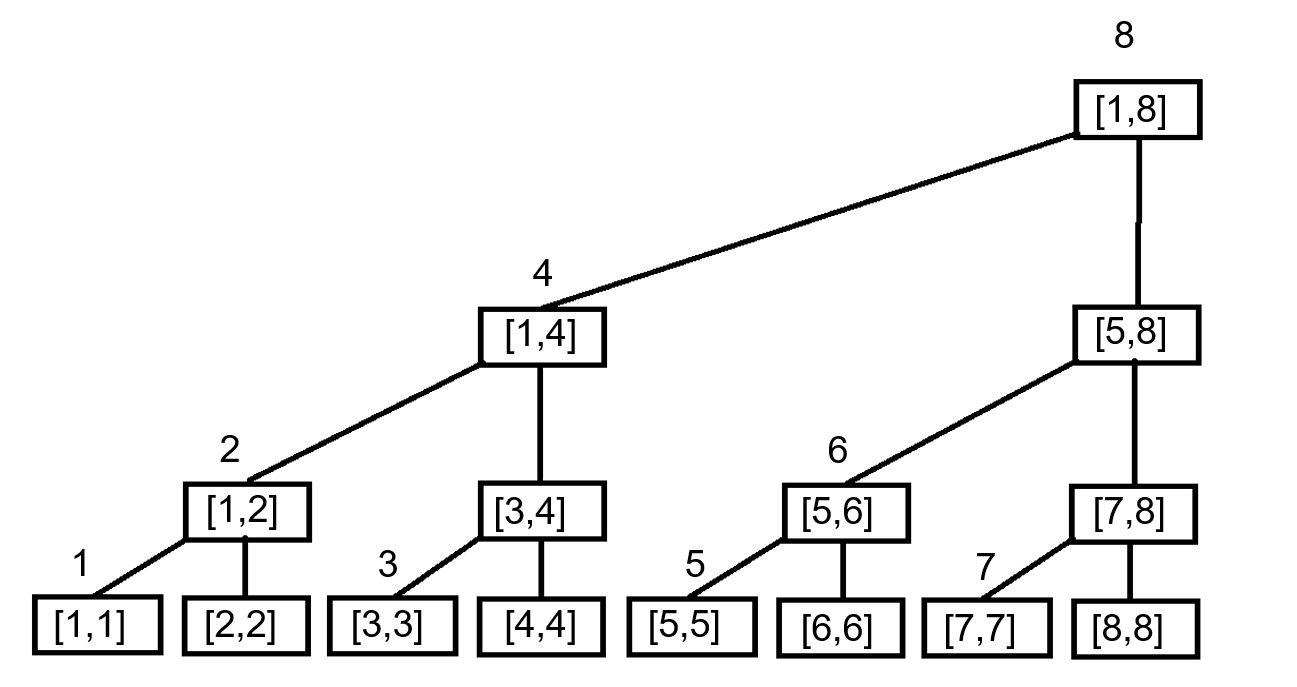
每个节点维护值的长度是该节点二进制最低位1代表的值。

树状数组中$lowbit$​函数是得到一个数的最低位1代表的值，比如$lowbit(5)=1,lowbit(4)=4$.

如果改变$x$位置的值，就加上该位置的$lowbit$，一直加到$n$，就维护了树状数组。

查询时反过来，从$x$位置开始，减去当前位置的$lowbit$，一直减到$1$，就得到$x$位置的前缀和。

树状数组1

int a[maxn],n,m;
ll tree[maxn];  //树状数组

int lowbit(int x) { return x & (-x); }

void add(int x,int k)
{
    for(int i=x;i<=n;i+=lowbit(i))
        tree[i] += k;
}

ll query(int x)
{
    ll ans = 0;
    for(int i=x;i;i-=lowbit(i))
        ans += tree[i];
    return ans;
}

int main()
{
    cin>>n>>m;
    for(int i=1;i<=n;i++)
        a[i] = read();
    for(int i=1;i<=n;i++)
        add(i,a[i]);
    int opt,x,y,k;
    while(m--)
    {
        opt = read();
        if(opt==1)
        {
            x = read(),k=read();
            add(x,k);
        }
        else if(opt == 2)
        {
            x = read(),y = read();
            printf("%d\n",query(y)-query(x-1));
        }
    }
    return 0;
}

区间修改，单点查询

区间修改用到差分数组的知识，若原数组为$a$,其差分数组为$b$，则$a[i] = b[1]+b[2]+\cdots +b[i]$.

若要修改原数组$[l,r]$区间上的值，比如都加$2$，只需要在差分数组中$b[l]$位置$+2$，$b[r+1]$位置$-2$即可。

由于树状数组维护前缀和，所以用树状数组维护原数组，用差分数组建树状数组，查询时直接查询即可。

树状数组2

int a[maxn],n,m;
ll tree[maxn];  //树状数组

int lowbit(int x) { return x & (-x); }

void add(int x,int k)
{
    for(int i=x;i<=n;i+=lowbit(i))
        tree[i] += k;
}

ll query(int x)
{
    ll ans = 0;
    for(int i=x;i;i-=lowbit(i))
        ans += tree[i];
    return ans;
}

int main()
{
    cin>>n>>m;
    for(int i=1;i<=n;i++)
        a[i] = read();
    for(int i=1;i<=n;i++)
        add(i,a[i]-a[i-1]);
    int opt,x,y,k;
    while(m--)
    {
        opt = read();
        if(opt==1)
        {
            x = read(),y = read(),k=read();
            add(x,k);
            add(y+1,-k);
        }
        else if(opt == 2)
        {
            x = read();
            printf("%d\n",query(x));
        }
    }
    return 0;
}

总结

虽说只是模板，但是线段树这两题还是写了很久，代码量巨大。不过也比之前理解地更清楚了，虽说线段树是很有用的工具，但对于我来讲估计用上它的概率不大，用上的也写不出(太菜了)。